FIR filter || Whitepaper
Introduction
The following whitepaper introduces you to the world of FIR filters. After a short general description of digital filters, the structure and function of FIR filters will be described and how to parameterize FIR filters in OXYGEN, so that you are able to cover your requirements with FIR filters using DEWETRONs software OXYGEN.
Digital filters – general
A digital filter is a mathematical algorithm for manipulating a signal to extract information and remove unwanted information, such as blocking or passing a certain frequency range. Thus, it is a digital system which converts an input sequence with a transformation process into an output sequence.
Digital filters are divided into two categories:
- Infinite impulse response (IIR)
- Finite impulse response (FIR)
As the names suggest, each filter type is categorized by the length of its impulse response. Unlike analog filters, which are implemented with electronic components such as capacitors, coils, resistors, etc., digital filters are implemented with logic devices such as ASICs, FPGAs or in the form of a sequential program with a signal processor.
IIR and FIR filters – what makes the difference?
As mentioned before digital filters are categorized according to the individual impulse response. The impulse response is the response of a filter to an input impulse: x[0]=1 and x[i]=0 for all i≠0.
If the impulse response of the filter drops to zero after a finite time has elapsed, it is referred to as an FIR filter (Finite Impulse Response). If, on the other hand, the impulse response is unlimited in time, it is an IIR filter (Infinite Impulse Response). Whether the impulse response of a digital filter drops to zero after a finite time depends on how the output values are calculated. With FIR filters, the output values depend only on the current and preceding input values, while with IIR filters the output values depend additionally on the preceding output values.
The advantage of IIR filters over FIR filters is that IIR filters typically require fewer coefficients to perform comparable filtering operations, operate faster, and require less RAM.
The disadvantage of IIR filters is their non-linear phase response. For applications that do not require phase information, such as monitoring signal amplitude, IIR filters are well suited. For applications that require a linear phase response, FIR filters are generally better suited.
FIR – Filter functional understanding
The following illustration is intended to demonstrate the functional operation of an FIR filter. At the input the data/values x(n) are applied by the A/D converter clock by clock (sample by sample).
In the upper row there are shift elements (z-1) which shift the data/values applied to the input by one step for each clock cycle. This means that at the end of the following example a value x(n-3) 3 clocks prior to the
current value x(n) is present.
In the center are the FIR coefficients k0 – km. These coefficients represent an amplifier that multiplies the inputvalue by the gain „k“.
In the lowest row is the summation branch which adds up the results of all multiplications (integration). The output is now the processed signal according to the FIR coefficients.
The output can be represented by following mathematical expression:
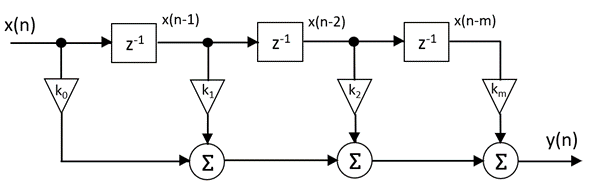
Fig. 1: Calculation process of a FIR filter
Example for determination of the filter coefficients of a FIR low-pass filter
To understand the determination of the FIR coefficients, we will now calculate them, using an FIR low-pass filter, as an example.
In the time domain, an analog signal can be described by its step response or by its impulse response. The impulse response is the derivative (differentiation, slope analysis) of the step response and vice versa the step response is the integration (summation) of the impulse response. Exactly the latter happens in a FIR filter. 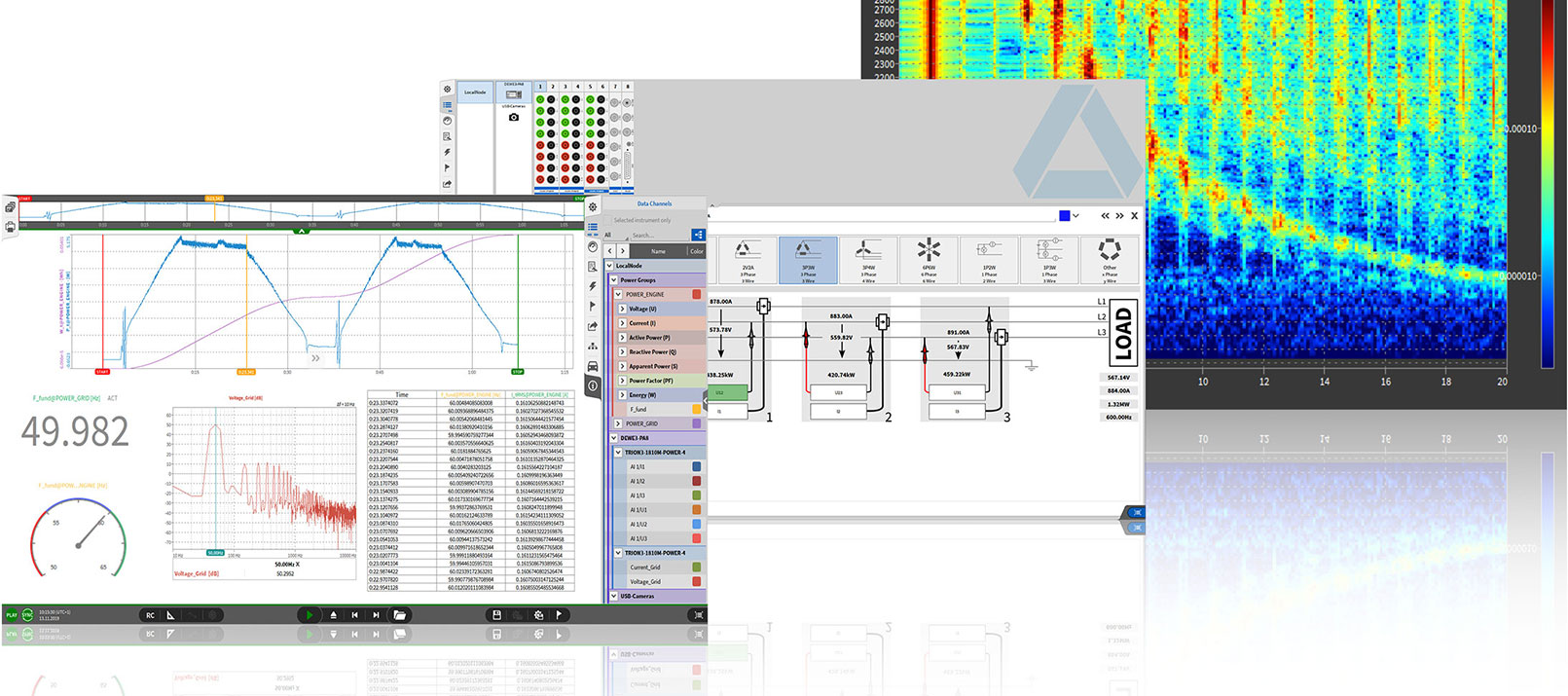The coefficients of the impulse response are stored in the calculator of the FIR filter. Since in the FIR filter the sum of the multiplications of the input value with the respective coefficients is formed at the output, in principle nothing else happens than an integration of the input signal over the impulse response.
The ideal low-pass filter is a sinc filter. The sinc function is defined as:
The impulse response (inverse Fourier transform of the transfer function of an ideal low-pass filter) of a filter is defined as:
Fig. 2: Calculation process of a FIR filter
In this case “fc” is the cut-off frequency, expressed as fraction of the sampling rate. For instance, if the sampling rate is 10kHz and the cut-off frequency is 1 kHz then fc = 0.1.
The problem is that the result of the inverse Fourier transform of the transfer function of an ideal low-pass filter is infinite, and in that case not realizable. To get a finite impulse response with the desired length N, a section of the infinite impulse response is selected by a window function.
In this case let’s use the well-known Blackmann window function (other window functions are available, see “WINDOW FUNCTIONS” in the following section), defined as:
Usually, α = 0.16 is selected for the classic Blackman window.
Fig. 3: Blackman window function
What we now must do, is to multiply the impulse response of a filter with the window function (Blackman in this case) to get the FIR filter coefficients (with the sinc filter shifted to the range [0, N−1]).
This results in the normalized windowed-sinc filter:
Fig. 4: Normalized windowed-sinc filter
How to set up an FIR filter in OXYGEN
OXYGEN has been extended by a very easy configurable variant for setting FIR filters. After the selection of the channel on which a FIR filter shall be configured, it is possible to add a FIR filter by selecting the option of the existing list of OXYGEN math functions.
Fig. 5: Adding an FIR filter channel in OXYGEN
You can choose between 4 different filter types:
- Low pass
- High pass
- Band pass
- Band stop
After pressing the “Add” button, there will be added a new FIR channel. If you open the settings of the channel you can set up your FIR filtered signal.
Fig. 6: Settings for an FIR filter channel in OXYGEN
Just enter the filter length, the desired window function, and the information if the signal delay, due to the filter length shall be compensated or not.
Additionally, it is possible for FIR lowpass filters to define different filter stages to reduce the calculation effort. This is very useful when, for example, a very low cut-off frequency is applied at a very high sampling rate. This would lead to a high filter length and due to the filter length, a high calculation effort and signal delay. By entering a decimation factor, the input sample rate will be reduced by the given factor. For instance, if you have a signal sampled with 200 kHz and you want to set up a low pass filter with a cut-off frequency of 100 Hz, it is advisable to add different stages. By entering a decimation factor of 2 for the first filter stage the sample rate will be reduced to 100 kHz.
By adding another stage with a decimation factor of 5 for instance, it will be reduced to 20 kHz. For the last stage in previous screenshot there has been entered a decimation factor of 20 to reduce the signal to 1 kHz, and the final cut-off frequency of 100 Hz.
Without this operation and by using only one filter stage it would be necessary for this example to use a filter length of about 5000 to get a similar response as with the mentioned filter stages and a filter length of 600. As a result, the individual filter stages are performed with lower filter lengths, which results in a reduction of the computational load. In addition, it also leads to a reduction of the signal delay since the filter length is only 3 times 600, i.e. 1800, instead of 5000 as in this example.
Window functions
In digital signal processing, a window function determines the weighting with which the samples obtained during the sampling of a signal within a section (window) are included in subsequent calculations. Outside of the interval the window function is zero.
In the filter design, wide window functions lead to steep transitions between passband and stopband, but to low stopband attenuation. Narrow window functions lead to flat transitions between passband and stopband, but to high stopband attenuation.
In OXYGEN there are several window functions available for you to choose from, to get the best result for your requirements:
- Rectangular
- Hann
- Hamming
- Blackman
- Blackman/Harris > Flat Top
- Bartlett
- Kaiser
- Cosine
DEWETRON – Your expert in measurement technology
DEWETRON is a specialist in the field of measurement technology. The goal is to produce measuring equipment that meets the highest possible quality standards, is modular and versatile, as well as easy to use.
If you want to learn more about DEWETRON, you can visit our DEWETRON website. There you will find further whitepapers as well as blogposts and video tutorials. We are also active on social media. Take a look at our Twitter, LinkedIn or YouTube pages.
