DQ analysis for rotary field machines
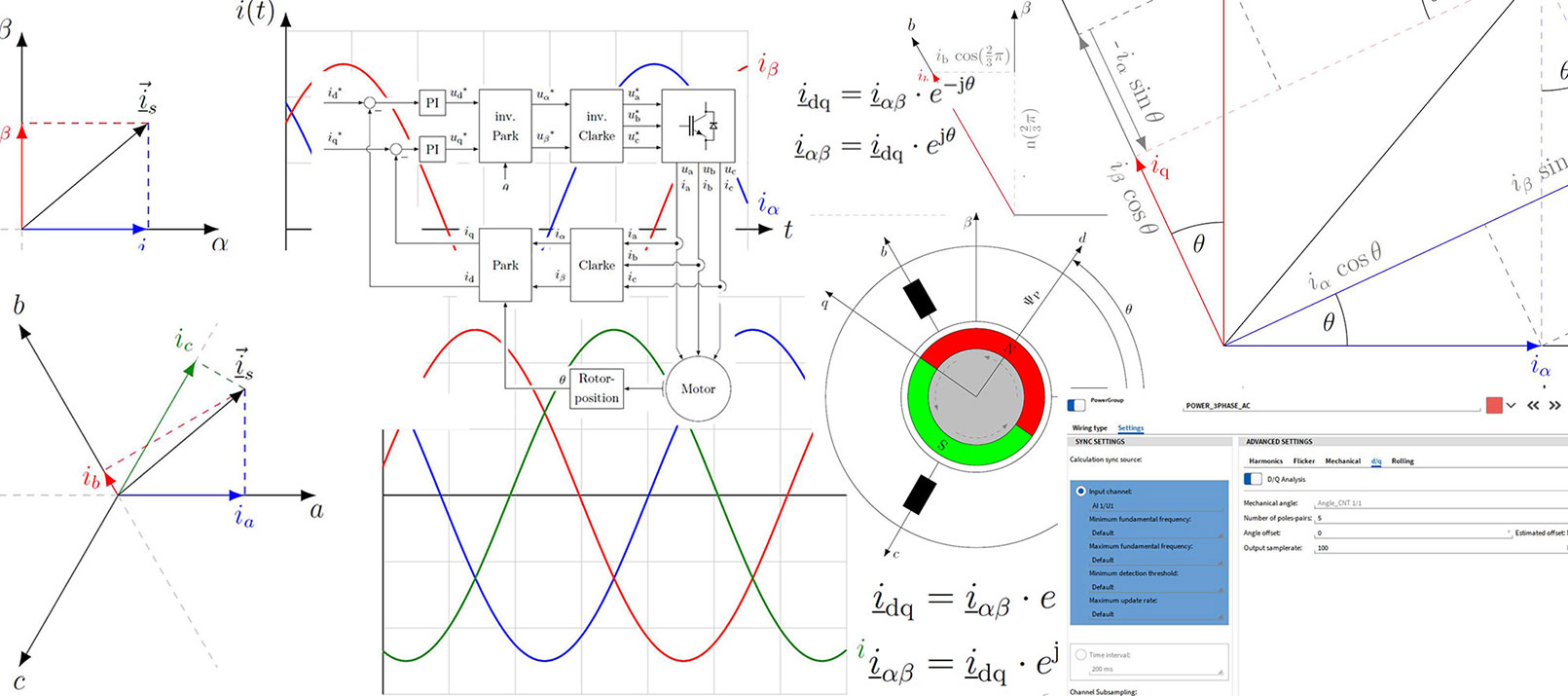
Introduction
The DQ analysis is used to convert the occurring alternating quantities in rotating field machines, such as electric currents, induced voltages or flux linkages, into constant quantities. This offers advantages for the analysis and control of electrical machines.
Find out in this whitepaper what the DQ analysis is and how our data acquisition solutions support you.
DEWETRON – Your expert in measurement technology
DEWETRON is a specialist in the field of measurement technology. The goal is to produce measuring equipment that meets the highest possible quality standards, is modular and versatile, as well as easy to use.