信号处理中的频率分析

许多物理现象(如振动、声学或电信号)本质上都是与频率相关的。在测量这些信号时,原始数据不仅包含主要信号本身,还包括噪声、共振和谐波等附加信息。这些特征参数在使用纯时域分析方法时往往难以识别,而通过频率分析则可以相对轻松地获取结果。
在本文中,我们将深入探讨频率分析的基础概念、常见方法、典型应用场景,以及我们的测量软件 OXYGEN 如何支持频域分析。
什么是频率分析?
为了更好地理解这个问题,我们先简单回顾一下信号处理的基本概念。在信号处理领域,连续信号通常不仅在时域中进行分析,也会在频域中进行分析。时域分析描述的是信号随时间的变化,而频率分析则揭示了信号中包含哪些频率成分,以及这些频率对整体信号的贡献程度。要全面理解一个测量信号,通常需要结合时域和频域两种视角。
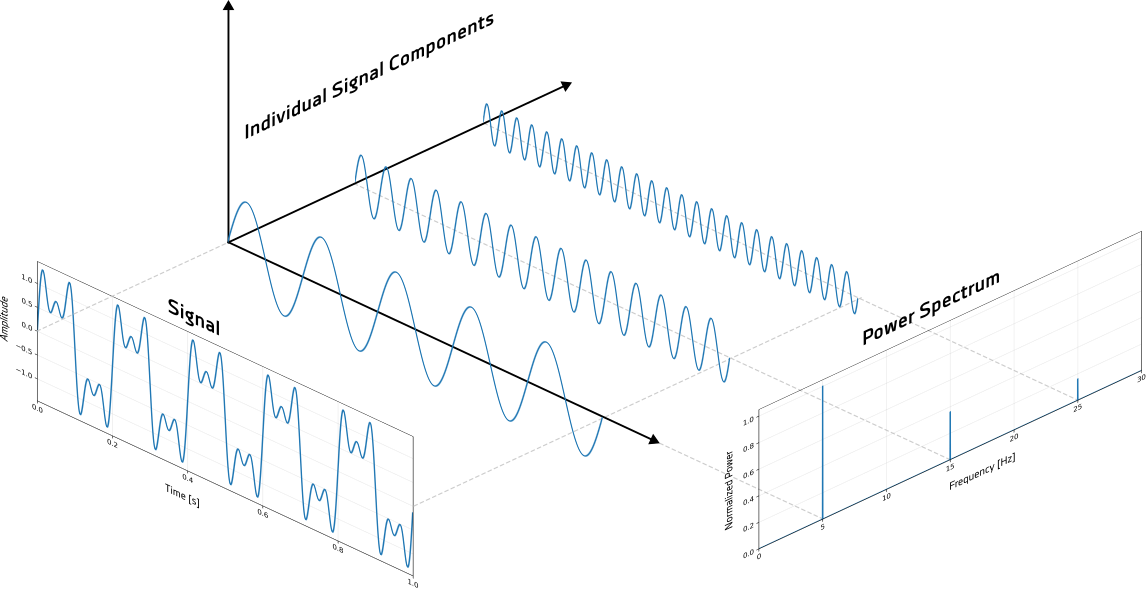
图1:信号在时域中的显示(左),分解为其各个分量(中),以及在频域中的可视化呈现(右)
那么,这在实际中意味着什么呢?简单来说,频率分析可以将复杂信号分解为其基本的频率成分。它不再关注信号随时间的变化,而是关注信号的频率组成。通过这种方式,可以识别周期性特征、主频率、谐波、共振频率等特征,而这些信息在原始时域数据中往往不容易获取。
频率分析是如何工作的?
分析信号频率内容的方法有很多种,具体选择哪种方法取决于应用场景以及需要提取的信息类型。有些分析侧重于识别主频率,有些则关注原始信号包含的频率成分如何随时间或运行条件变化。
在所有频率分析方法中,傅里叶变换(Fourier Transform) 以及其高效实现形式——快速傅里叶变换(FFT),是最基础也是最常用的工具。
什么是快速傅里叶变换(FFT)?
快速傅里叶变换(FFT) 是一种数学变换方法,用于将时域信号转换为频域信号来进行显示。与展示信号随时间变化方式不同,FFT 显示的是信号中包含哪些频率成分,以及各个频率的强度。
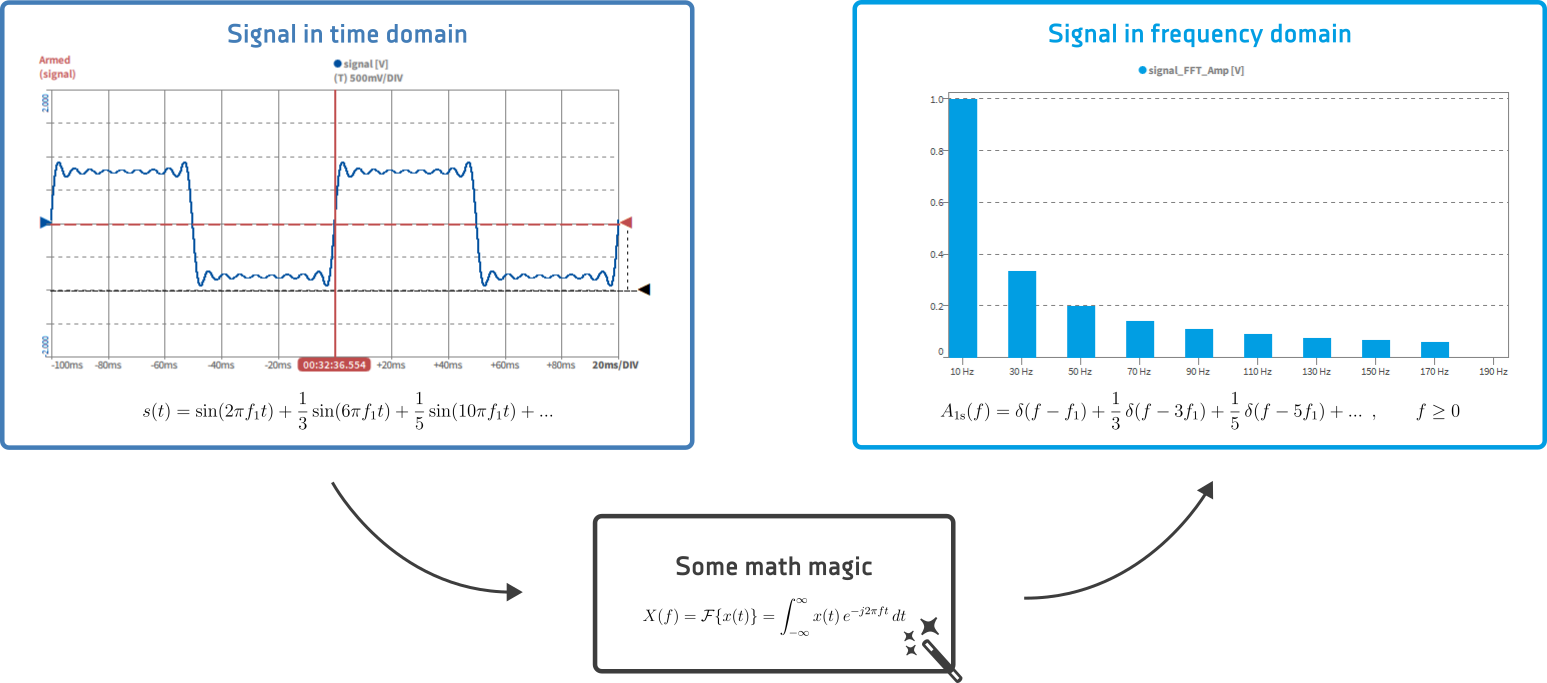
图2:左:由多个正弦波分量组成的矩形信号;中:时间域到频率域的傅里叶变换;右:仅显示正频率的一侧频谱图
FFT 是一种高效算法,即使在处理大量数据时,也能快速完成计算。其结果通常以幅值谱或功率谱的形式呈现。
常见的数学工具与分析方法
许多高级频率分析方法都是基于 FFT,并结合额外的数学处理,以获得更深入的分析结果。常见的方法包括:
- 幅度谱和功率谱
显示不同频率对信号的贡献强度,便于识别主频和谐波。 - 频谱色图(Spectrogram)
展示信号频率成分随时间的变化,将时间和频率信息显示在同一图中。 - 阶次分析与谐波分析
按转速或基频分析频率成分,常用于旋转机械和电力系统。 - 频域滤波
用于提取或抑制特定频率范围,从而突出关键信号或减少噪声干扰。 - 加窗与平均技术
通过减少噪声和频谱泄漏,提高频谱分析的精度和稳定性。
频率分析的应用场景与意义
频率分析在涉及动态、振荡或周期性特征场景的应用中尤为重要。它能够揭示时域中难以发现的信息,因此被广泛应用于多个行业和领域。
汽车与交通
- 发动机、传动系统和电机的 NVH 分析
- 识别与转速相关的效应和共振
航空航天与结构测试
- 模态分析与共振识别
- 结构振动与疲劳分析
电力与能源
- 电网中的谐波分析
- 识别电能质量问题和系统扰动
工业制造与运行状态监测
- 轴承或齿轮故障的早期检测
- 基于频率的设备健康监测
声学与噪声分析
- 识别主要噪声源
- 评估频率加权声级
科学研究
- 天体物理学中的周期信号分析
- 地震学中的地震波分析及地下结构研究
医学
- 心电图(ECG)和脑电图(EEG)分析
- 超声信号和生理节律评估
通信技术
- 调制方案和信号带宽分析
- 干扰、噪声和频谱拥塞检测
使用 OXYGEN 进行频率分析
信号采集、处理和分析是我们的核心能力,因此我们的测量软件 OXYGEN 提供了全面的频率分析工具。
从直观易用的分析与可视化工具(如频谱分析仪和频谱图),到灵活的滤波功能,用户可以轻松提取关键频率范围或抑制不需要的信号成分。
此外,OXYGEN 还支持多种分析方法,包括 FFT、STFT 和 CPB 分析,以及更高级的应用,如模态测试、阶次分析、声级分析等。
如需了解 OXYGEN 在频率分析方面的完整功能概览,欢迎下载我们的专属一页式介绍资料: